【数学】虚数・複素数について　初歩

ということで虚数のお話しです。

虚数とはその昔1６世紀、イタリアの数学者ジローラモ・カルダノによって書かれた『アルス・マグナ』によってはじめて世に出たとされています。

通常、同じ数を掛け算すると＋になりますよね。要は2乗すると＋になるってこと

2乗すると－の値になるものを指します。正確には2乗すると-1になるものを虚数といいます。

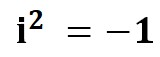
後にフランスの哲学者のデカルトによって『nombre imaginaire』（想像上の数）と呼ばれ。

これが虚数（imaginary namber）の語源となったそうです。

なので虚数はよく imaginary の頭文字から　i　を用いて表します。これはスイスのレオンハルト・オイラーによって名付けられたと言われます。

※虚数がどのように誕生したのかは暇があれば書きます

虚数は実用性が無い？

実際に存在しない数はなぜ使う必要があるのか。

ありえない数字というのは、実際にはありえないけど言葉を数式で表すために必要なことだということです

例えばカルダノは

A+B＝１０
A×B＝４０
となるAとBの数を答えろ

といった難問を出しています。

普通に計算しても出てこないのです。これを証明するには虚数の存在を過程しなければなりませんでした

詳しくは長くなるので割愛しますが解の公式を使うと答えはA=５＋√-15　B=５－√-15　となります。

√-15というのはルートの中にマイナスが入っているのであり得ないのです、この部分が虚数ということです。

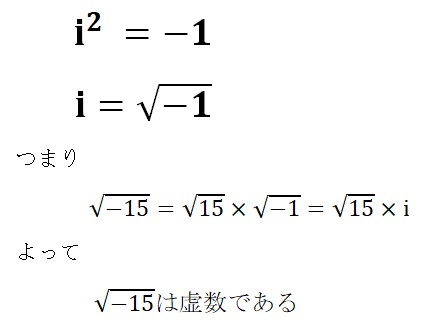
上記で示しましたが解の中に虚数が出てきました。

これが何の意味があるのか…
カルダノは当時著書『アルス・マグナ』で本人は詭弁だとし、使い道なんてないと書いているそうです。

ですが

時は流れてその虚数の持つ力はただ詭弁ではなかったということがわかってきます。

虚数は
波の持つ特性を説明する際に使われたり、電子のふるまいの説明するときや宇宙についても
虚数を使って説明できることはたくさんあるそうです。シュレディンガーや、アインシュタイン、ホーキングなどの偉人も
虚数を使った量子力学や宇宙の解明などに触れています。（僕は詳しく知らないけど）
とても都合が良いそうですねー
うーん…本当にこれを思いついた人達すごすぎます。。。

虚数の使われ方①

それは先に答えを言うと

回転と拡大

です。なんで？ってなりますがそれは説明していきます。

数学の世界で虚数は、虚数と実数が混ざった形で使用されます。

そうした虚数＋実数のような形のものを複素数と言います。

3 　、　√２ 　、　 π 　実数（有理数や無理数）
i 　、　2i　 、 　5i　　 虚数（iを含む数）
3+i 、 -4+5i 、 2-7i　　複素数(虚部は０ではないこと)

ちなみに実部と虚部というのは下の図になります。

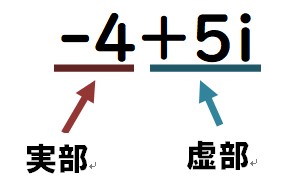
虚数の使われ方②　　虚数を使った回転

さて

この複素数を利用してどうやって回転と拡大を表すのか

その前に実数軸で一つ考えてみてほしいことがあります。
実数軸の正方向に１進んだ場所に点があるとします。
１に-1をかけるともちろん座標は-1になりますよね？
これ、考え方を変えると180度反転（回転）していると思いませんか？

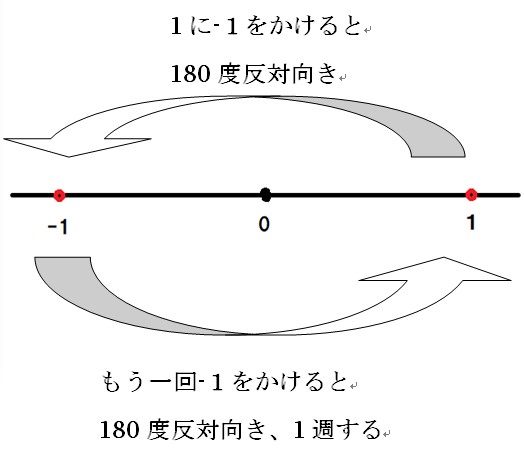
では虚数とはなんでしたっけ
iを2乗したら-1になる数でしたよね
2回かけて-１になるのです
-１かけると180度向きが変わるのなら

iを2回かけると180度向きが変わるのとおんなじことですよね

つまりiを一回かけると角度が90度変わるということです。

虚数『i』をかけると向きが90度変わる。

このことを18世紀くらいにガウスやヴェッセルがあみだした「複素平面（ガウス平面）」を使用して説明ができます。

ガウスやヴェッセルは実数軸を横に引き、存在しない虚数を虚軸として縦軸を引きました

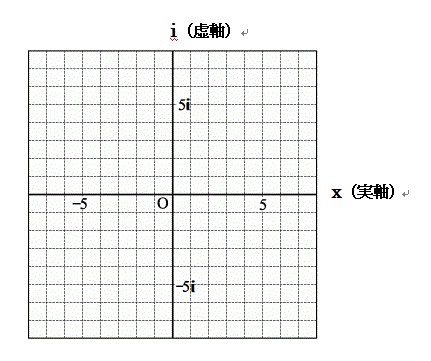
お約束として虚軸方向へは虚数のiが常についてまわります。

ではここに例としてA（2,3i）というのをプロットしてみましょう

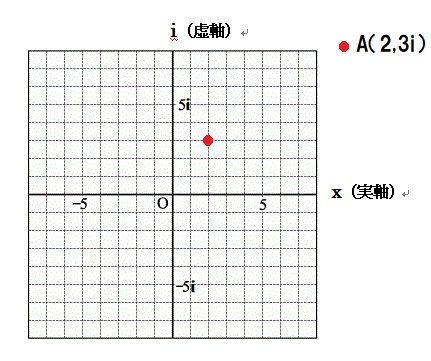
このようになります
では早速虚数『i』を座標にかけてみましょう
本当に90度回転が起きるのでしょうか

A（2,3i）×i　→　B（2i,-3）
※今回座標の書き方は（実軸、虚軸）ではありません
iが付いていたら虚軸だと思ってください。

その点をBとしてプロットしてみますと

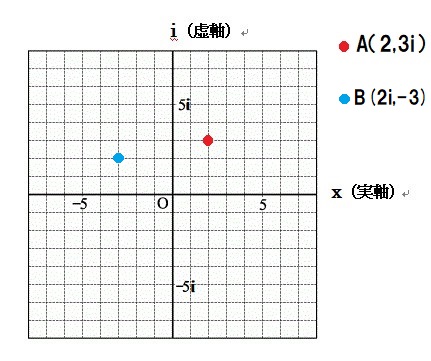
はい、プロットしました、それぞれの座標の位置関係はこの通りです。
もうわかったと思いますが

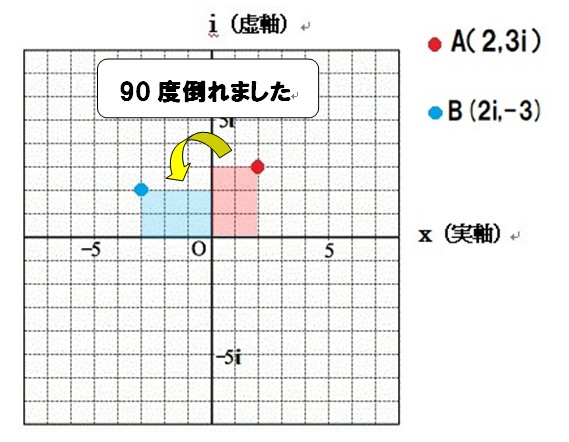
そうです、ちゃんと90度回転しています。
同じように虚数iをかけていくと90度づつ回転していき、4回かけると元に戻ります。
これで回転していることがわかりました。

※90度ではなく45度とか回転させたい場合は三角関数の知識を利用します、今回は割愛します

虚数の使われ方③　　虚数を使った回転拡大

では拡大をしていきます

先ほどの点Aを90度回転してなおかつ2倍に拡大していきます
簡単です、iを2倍した2iをかければよいのです。
やってみましょう

A（2,3i）×2i　→　C（4i,-6）

プロットしてみますと

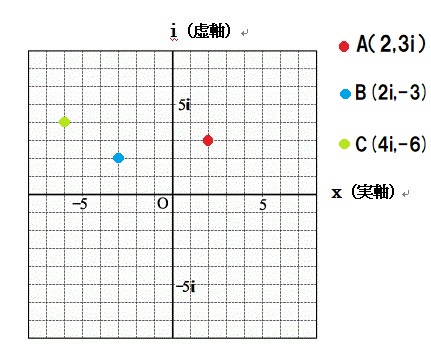
そして、比較してみます

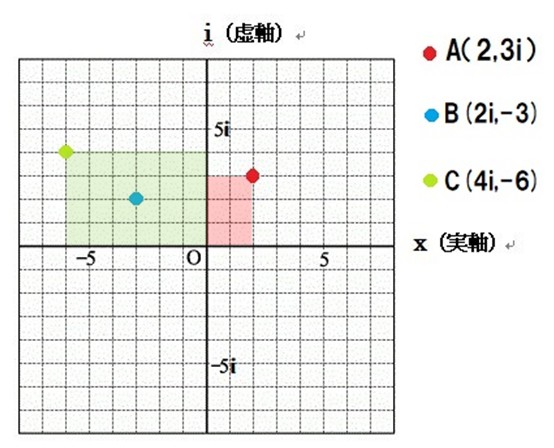
こんな感じですね。

一片の長さが2倍された四角形が見えますが
面積2倍になりました、しっかり90度回転してます。
※面積を出しているのはわかりやすくするための措置です

ちょっと重ねてみましょう

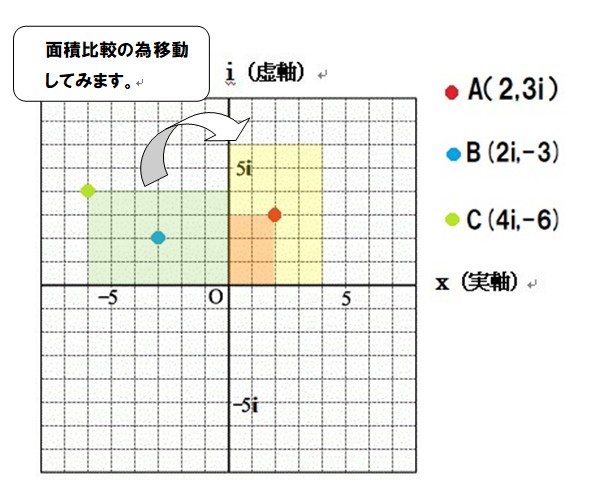
黄色の四角が回転のみ戻したものです
しっかり面積も2倍です、もちろん原点から点A、原点から点Cのスカラーも2倍

※スカラーとはベクトル量と違い向きを考慮しない単純な量（大きさ）のことです
実際回転してるのでベクトルは違うので量の比較の為スカラーとしています。

これで虚数が回転と拡大にかかわっていることがわかりました。

僕は専門家じゃないので、もっと専門的でとことん理解したい人には申し訳ない内容ですが。
虚数を知ることで、数学は答えの決まった学問として解いていた自分の考えが少し変わりました。
答えを導くために仮定・仮設を立てることの大切さ。その仮説が正しいことを証明すること。
なんだか少し頭が良くなった気分になりましたｗｗｗ
…ということでここいらでいったん終わりにしますー

ということで時間があったら実際に使われている例を見ていこうと思います。

ここはこう書いたほうが良いとかありましたらこっそりメールで教えてくださいー